Bellman-Ford:负权值最短路径

2019-09-03

关于 Bellman-Ford 算法

Bellman-Ford 算法是解决单起点最短路径问题的一种算法，由 Lester Ford 发表于1956年，Richard Bellman 发表于1958年。他和 Dijkstra 算法比较相似，都以松弛为基础。然而，Dijkstra 算法每次仅对收录点的出边的终点进行松弛，无法处理路径中的负边对已收录点的连锁影响（知乎上有详细解释 (= . =)，这里就不细说了）。Bellman-Ford 算法牺牲了一定的时间复杂度，实现了对负边最短路径的处理。

算法核心

Bellman-Ford 算法的核心是遍历和松弛，每次循环遍历每一条边进行松弛，总共进行n-1次。

说的详细一点(= . =)。对于每一轮循环，尝试使用每一条边进行松弛。由于边的顺序随机，因此对于每一个点，可能出现以下四种状况：

该点已经找到最短路径。没有一条边可以使该点的最短路径减小。
恰巧仅走过一条边后该点可以找到最短路径。无论边如何排列，一次循环可以使该边找到最短路径。
走过两条及以上边后该点才可以找到最短路径，但这些边恰巧按经过的先后顺序排列（或部分按顺序排列）。一次循环可以按顺序对该点的最短路径进行多次松弛，增加多条边（如下图第三步）。这种情况比较接近于 Dijkstra 算法，但 Dijkstra 算法是使用贪心主动寻找最短边，使边按顺序被处理，而此处则是一种随机状况。
走过两条及以上边后该点才可以找到最短路径，但这些边不按经过的先后顺序排列，对后经过的边的处理先于先经过的边。一次循环仅可以进行一次松弛增加一条边，而其余的则需要等待下一次循环处理（如下图第二步）。这种情况下，无差别遍历不会受到已有路径的干扰，有效地解决了负边的影响。

由于最短路径最多只会经过每一个点一次（若经过一次以上则说明成负权值环，没有最短路径），即除起点外共走过 n-2 个点，n-1 条边，因此，即使某条最短路径需要走过每一个点且每次循环只给此最短路径进行一次松弛，增加一条边，最多只需要进行 n-1 轮循环就一定能找到最短路径。

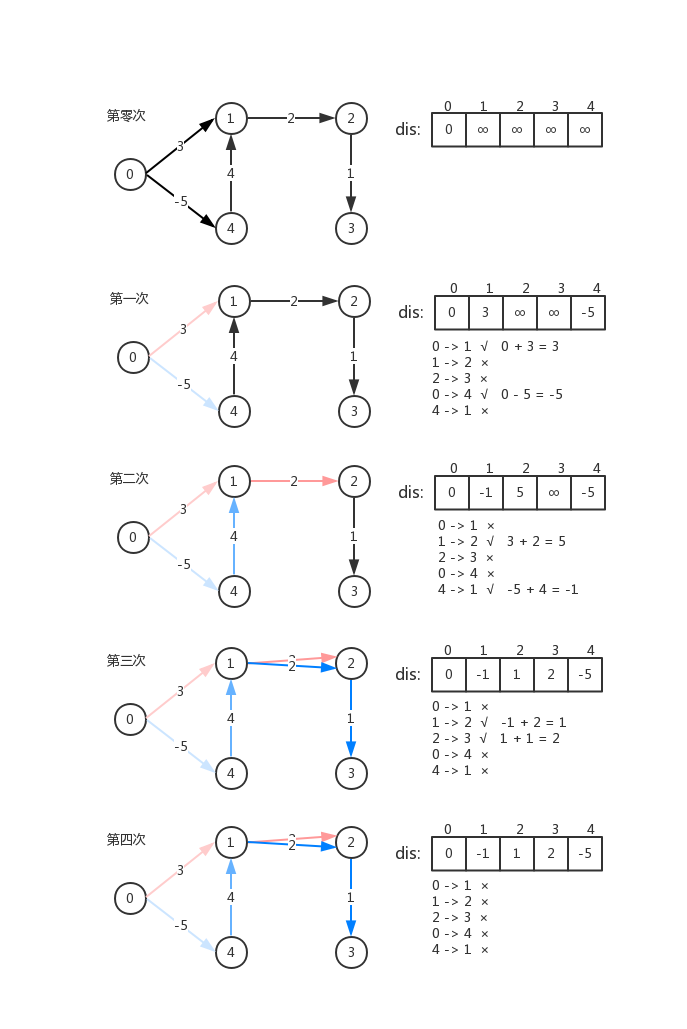
假设图有n个点，m条边。使用大小为 m 的三个数组来存边的信息，u[] 储存边的起点， v[] 储存边的终点， w[] 储存边长。并使用大小为 n 的数组 dis[] (distance) 储存起点到各点的距离，其中起点到自己的距离为 0。代码包含二层循环，外层循环共 n - 1 轮，每次循环多加一条边。内层循环 m 轮，每次循环判断一条边能否改变最短路径，若能，则更新最短路径。

具体代码如下：

//算法核心
for (int i = 0; i < n - 1; i++)
    for (int j = 0; j < m; j++)
        if (dis[v[j]] > dis[u[j]] + w[j])
            dis[v[j]] = dis[u[j]] + w[j];

Bellman-Ford 算法的时间复杂度为 O(N * M)。

优化

提前跳出

若一次遍历没有更新任何一个最短路径，则说明在已有的最短路径上添加任何一条边都无法使最短路径变短，已有的数据已经达到了最短路径。此时就可以提前跳出循环，降低复杂度，使算法拥有最低为 O(M) 的时间复杂度。因此，可以添加一个值 check 来判断一次循环是否更新了最短路径。

具体代码如下：

//算法核心 + 检测
int check = 0;
for (int i = 0; i < n - 1; i++) {
    for (int j = 0; j < m; j++)
        if (dis[v[j]] > dis[u[j]] + w[j]) {
            dis[v[j]] = dis[u[j]] + w[j];
            check = 1;
        }
    if(check == 0)
        break;
}

检测负权环路

若已经经过 n-1 次遍历，再次遍历时仍有边能进行松弛，则说明图中有负权值的环路。因为此时进行松弛的路径已经包含了最少 n 条边 n + 1 个点，这说明图中一定形成了环路。去除正权值环路会使路径减小，因此在此最短路径中一定不存在正权值环路，此环路一定为负。在完成核心算法后再次遍历尝试松弛即可检验出该图是否含有负权值环路。

具体代码如下：

//检测负权值回路
int flag = 0;
for(int i = 0; i < m; i++){
    if (dis[v[i]] > dis[u[i]] + w[i]) {
        flag = 1;
    }
}
if(flag == 1)
    printf("有负权值环");

队列优化

队列优化的原理是，每次仅尝试给最短路径发生改变的路径添加新的边，即每次只遍历以发生变化的路径的终点为起点的边。因此需要一个队列来存储当前各路径的终点，每次循环遍历队列头部点的边进行松弛，将最短路径改变的点加入队列尾部（若该点不在队列中），直到没有点的最短路径发生改变为止。

由于已入队的点重复入队会造成没有任何意义的重复探查，因此使用大小为 n 的数组 book[] 来记录每个点是否在队列中。此处使用邻接矩阵 mx[n][n] (matrix) 存储图的信息，这样访问每个点的出边的时间复杂度最小。使用数组 q[]（queue）和指针 head、tail 表示队列。

具体代码如下：

//队列优化
while(head != tail){
    for(int i = 0; i < n; i++){
        if(dis[i] > dis[q[head]] + mx[q[head]][i]) {
            dis[i] = dis[q[head]] + mx[q[head]][i];
            if(book[i] == 0){
                book[i] = 1;
                q[tail] = i;
                tail++;
            }
        }
    }
    book[head] = 0;
    head++;
}

经过优化以后，算法的时间复杂度最小为 O(M)，最坏情况仍为 O(N * M)。

参考资料

1.《啊哈算法》(2014): Bellman-Ford —— 解决负权边

2.《啊哈算法》(2014)： Bellman-Ford 的队列优化